|
Volume Conversion To Metric Calculator
The volume of any solid, plasma, vacuum or theoretical object is how much three-dimensional space it occupies, often quantified numerically. One-dimensional figures (such as lines) and two-dimensional shapes (such as squares) are assigned zero volume in the three-dimensional space.Volume is presented as ml or cm3.
Volumes of straight-edged and circular shapes are calculated using arithmetic formulae. Volumes of other curved shapes are calculated using integral calculus, by approximating the given body with a large amount of small cubes or concentric cylindrical shells, and adding the individual volumes of those shapes. The volume of irregularly shaped objects can be determined by displacement. If an irregularly shaped object is less dense than the fluid, you will need a weight to attach to the floating object. A sufficient weight will cause the object to sink. The final volume of the unknown object can be found by subtracting the volume of the attached heavy object and the total fluid volume displaced.
Volume Formulas
| Shape |
Equation |
Variables |
| Cube: |
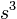 |
s = length of any side |
| Rectangle Prism: |
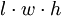 |
l = length, w = width, h = height |
| Cylinder: |
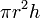 |
r = radius of circular face, h = height |
| Prism: |
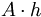 |
A = area of the base, h = height |
| Sphere: |
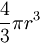 |
r = radius of sphere which is the
integral of the Surface Area of a sphere |
| Ellipsoid |
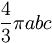 |
a, b, c = semi-axes of ellipsoid |
| Pyramid: |
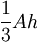 |
A = area of the base, h = height of pyramid |
| Cone: |
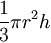 |
r = radius of circle at base, h = distance from base to tip |
Note: The units of volume depend on the units of length - if the lengths are in meters, the volume will be in cubic meters, etc.
|